Topological Sorting – Wkipedia
In the field of computer science, a topological sort (sometimes abbreviated toposort) or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed a cyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time.
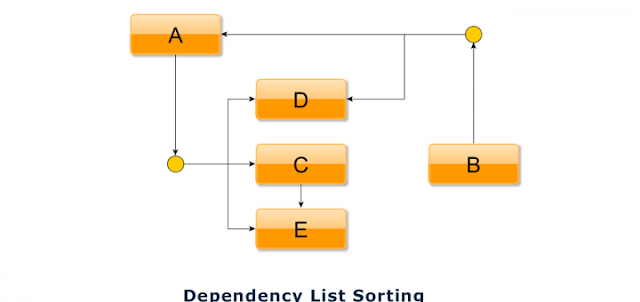
Topological Sorting – Practical Case:
In a system I was working, I faced the problem as some of the modules in the system depends on some others. So at the moment of execution, those modules has to be loaded to have every module working. Consider plugins, where one plugin may depend on another. For example, a plugin that enables user actions such as like-dislike etc. on contents may need the contents plugin to be executed first.
Topological or Dependency list sorting in PHP:
First take a look at the following lines of codes
Using the above function is easy, just send an array of items as the first parameter and an array of dependency among the items as the seconds parameter.
In return, you get the sorted array of items or FALSE on failure.
For complete documentation read the README.md in github repository for Topological Sorting